AVL Tree / Data Structure

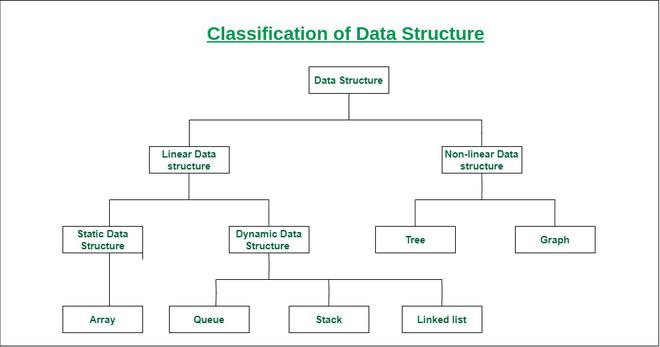
AVL Tree veri yapısını incelerken öncesinde Tree veri yapısını ve özelleştirilmiş çeşitlerine göz atmak faydalı olacaktır. Diğer yazılarımızda bu veri yapıları anlatılarak örneklendirilmiştir.

AVL Tree, Adelson-Velsky ve Landis matematik ve bilgisayar bilimcilerinin isimlerinden esinlenerek oluşturulan binary tree veri yapılarının özel kontrollerle dengelenmiş halidir.

Dengeleme işlemlerini yaparken bazı kavramlar devreye girmektedir. Bunlardan en önemlisi balance factory(dengeleme faktörü), oluşturulan alt ağaçlar arasındaki derinlik farkının en fazla '1' olmasını temsil etmektedir. Alt ağaçlar oluşturulurken belirlenen root düğümün sol altında root değerinden küçük varlıklar, sağ alt ağacından ise root değerinden büyük varlıklar sıralanmaktadır.

Özellikle arama işlemlerinde binary search tree veri yapısına göre avantajlıdır ancak eleman ekleme işlemlerinde dezavantajlıdır diyebiliriz.

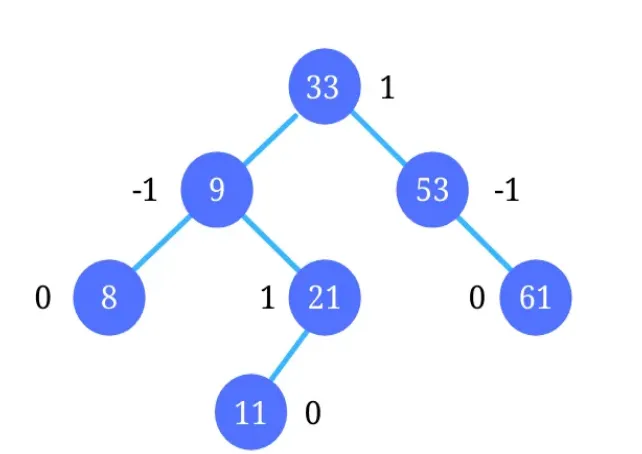
balance_factory = height(node.left) - height(node.right);

• Yukarıdaki matematiksel denklem kullanılarak AVL Tree veri yapısındaki dengelenme yönteminde bazı operasyonlar yapılmaktadır. Sol alt ya da sağ alt ağaç dengesizliği oluştuğunda bu dengeleme faktörü baz alınarak ağaç dengelenmektedir. Hadi bunu örneklendirelim hemen...

#include <iostream>
#include <memory> 
#include <algorithm>

using namespace std;

class AVLNode {
public:
    int m_data{};
    shared_ptr<AVLNode> m_left{}; 
    shared_ptr<AVLNode> m_right{}; 
    
public:
    AVLNode(int data, shared_ptr<AVLNode> left, shared_ptr<AVLNode> right) 
            : m_data(data), m_left(left), m_right(right) {}
};

class AVL {
private:
    shared_ptr<AVLNode> m_root{}; 

public:
    AVL(){}

    bool is_empty() const
    {
        return !m_root;
    }
};

int main()
{
    AVL avl;
    
    cout << boolalpha << avl.is_empty() << endl;
    
    return 0;
}
***************************************  
AÇIKLAMA : bu örnekte temel yapı oluşturulmuş ağaca hiç bir varlık eklenmediğinden boş olup olmadığını sorguladık. 
***************************************  
CEVAP : true
***************************************

• AVL Tree binary tree veri yapısının belirli dengesizlikler oluştuğunda yapılan işlemlerle dengelenmiş halidir demiştik. Bu dengesizlik çeşitlerini belirleyelim.

Single 1. Left-Left 2. Right-Right

Double 1. Left-Right 2. Right-Left

#include <iostream>
#include <memory> 
#include <algorithm> 
#include <iomanip>

using namespace std;

template<typename T>
class AVLNode {
public:
    T data;
    shared_ptr<AVLNode<T>> left;
    shared_ptr<AVLNode<T>> right;

    AVLNode(T data, shared_ptr<AVLNode<T>> left = nullptr, shared_ptr<AVLNode<T>> right = nullptr) 
        : data(data), left(left), right(right) {}
};

template<typename T>
class AVL {
private:
    shared_ptr<AVLNode<T>> m_root;

private:
    int height(shared_ptr<AVLNode<T>> node) const
    {
        if (node) 
        {
            int left{ height(node->left) };
            int right{ height(node->right) };

            return std::max(left, right) + 1;
        }
        else
        {
            return 0;
        }
    }

    shared_ptr<AVLNode<T>> insert(shared_ptr<AVLNode<T>> start, const T& data)
    {
        if (start) 
        {
            if (data < start->data)
            {
                start->left = insert(start->left, data);
            } 
            else if (start->data < data)
            {
                start->right = insert(start->right, data);
            }
        } 
        else 
        {
            return std::make_shared<AVLNode<T>>(data);
        }

        return start;
    }

    int diff_get(shared_ptr<AVLNode<T>> node) const 
    {
        return height(node->left) - height(node->right);
    }

    shared_ptr<AVLNode<T>> ll_rotate(shared_ptr<AVLNode<T>> node)
    {
        shared_ptr<AVLNode<T>> temp{ node->left };
        
        node->left = temp->right;
        temp->right = node;

        return temp;
    }

    shared_ptr<AVLNode<T>> rr_rotate(shared_ptr<AVLNode<T>> node) 
    {
        shared_ptr<AVLNode<T>> temp{ node->right };
        
        node->right = temp->left;
        temp->left = node;

        return temp;
    }

    shared_ptr<AVLNode<T>> lr_rotate(shared_ptr<AVLNode<T>> node)
    {
        node->left = rr_rotate(node->left);
        return ll_rotate(node);
    }

    shared_ptr<AVLNode<T>> rl_rotate(shared_ptr<AVLNode<T>> node)
    {
        node->right = ll_rotate(node->right);
        return rr_rotate(node);
    }
    
    shared_ptr<AVLNode<T>> balance(shared_ptr<AVLNode<T>> node)
    {
        int balance_num{ diff_get(node) };
        
        if (balance_num > 1) 
        {
            if (diff_get(node->left) > 0) 
            {
                cout << "ll_rotate - balance_num : " << balance_num << " and node : " << node->left->data << "\n";
                return ll_rotate(node);
            }
            else 
            {
                cout << "lr_rotate - balance_num : " << balance_num << " and node : " << node->left->data << "\n";
                return lr_rotate(node);
            }
        }
        else if (balance_num < -1) 
        {
            if (diff_get(node->right) < 0)
            {
                cout << "rr_rotate - balance_num : " << balance_num << " and node : " << node->right->data << "\n";
                return rr_rotate(node);
            }
            else 
            {
                cout << "rl_rotate - balance_num : " << balance_num << " and node : " << node->right->data << "\n";
                return rl_rotate(node);
            }
        }
        
        return node; //already balanced
    }
    
    void print_helper(shared_ptr<AVLNode<T>> node, int indent = 0) const 
    {
        if (node != nullptr) 
        {
            print_helper(node->right, indent + 4);
            cout << std::setw(indent) << "" << node->data << endl;
            print_helper(node->left, indent + 4);
        }
    }

public:
    AVL() : m_root(nullptr) {}

    bool is_empty() const 
    {
        return !m_root;
    }

    int height() const
    {
        return height(m_root);
    }

    void insert(const T& data) 
    {
        m_root = insert(m_root, data);
        m_root = balance(m_root); 
    }
    
    void print() const
    {
        print_helper(m_root);
        cout << "***************************";
    }
};

int main() 
{
    AVL<int> avl;
    
    cout << "Is AVL empty  : " << boolalpha << avl.is_empty() << "\n";
    
    avl.insert(33);
    avl.insert(53);
    avl.insert(15);
    avl.insert(19);
    avl.insert(20);
    avl.insert(25);
    avl.insert(26);
    avl.insert(28);
    avl.insert(18);
    avl.insert(17);
    
    cout << "\nHeight of AVL : " << avl.height() << "\n***************************\n";
    
    avl.print();

    return 0;
}
***************************************  
AÇIKLAMA : 
***************************************  
CEVAP : 
Is AVL empty  : true
lr_rotate - balance_num : 2 and node : 15
rl_rotate - balance_num : -2 and node : 33
rl_rotate - balance_num : -2 and node : 33
ll_rotate - balance_num : 2 and node : 20

Height of AVL : 5
***************************
            53
        33
                28
            26
    25
20
    19
            18
                17
        15
***************************
***************************************