Graph / Data Structure

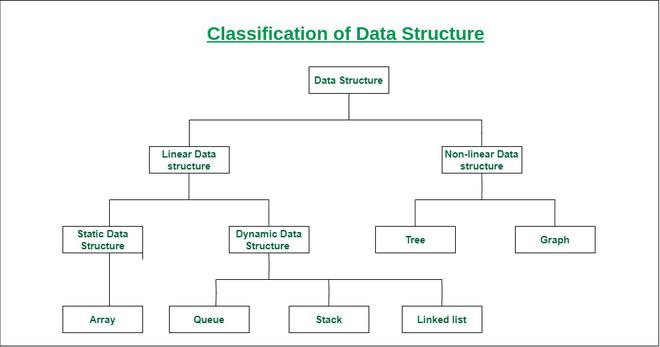
Veri yapıları linear ve non-linear olarak temelde iki ana başlıkta incelenmektedir. Bugün iki non-linear veri yapısından biri olan graph data structure karşılaştırmalı olarak ele alınacaktır.

Non-linear olan diğer veri yapısı tree ile arasındaki farklılıklara da değinerek örneklendirmeye geçeceğiz. Tree yapısını ayrı bir yazıda ayrıntılı ele alınacaktır.

• Yüzeysel olarak farklılıkları madde madde yazmaya çalışalım.

1. Graph veri yapısında her düğümün(node) herhangi sayıda kenarı(edge) olabilirken, Tree veri yapısında n node için (n - 1) edge olacaktır.

2. Graph veri yapısı directed ya da undirected olabilirken, Tree veri yapısı her zaman directed olacaktır.

3. Graph veri yapısı root olarak unique bir node yokken, Tree veri yapısında unique bir root node bulunur.

4. Graph veri yapısı döngüsel yapıda olabilirken, Tree veri yapısında herhangi bir döngü olmayacaktır.

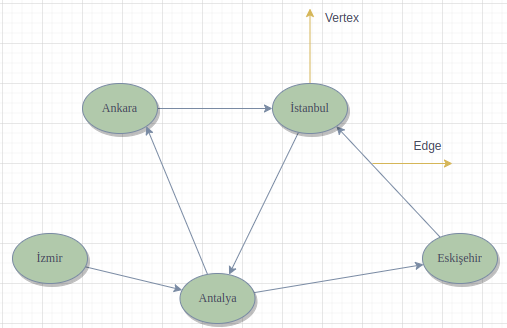
Bir sosyal ağ, kullanıcıları ve kullanıcıların birbirleriyle olan ilişkilerini temsil eden graph veri yapısıdır.

Hava yolları ağı, havaalanlarını ve bunları birbirine bağlayan uçuşları temsil eden graph veri yapısıdır.

Haritalar, şehirleri ve bu şehirleri birbirine bağlayan yolları temsil eden bir graph veri yapısıdır.

#include <iostream>
#include <unordered_map>
#include <unordered_set>
#include <vector>

// A : Airport type
// F : Flight type

template<typename A, typename F>
class AirlineNetwork {
private:
    unordered_map <A, vector<pair<A, F> > > adjacency_list;

public:
    void add_airport(const A& airport) 
    {
        if (adjacency_list.find(airport) == adjacency_list.end()) 
        {
            adjacency_list[airport] = vector<pair<A, F>>();
        }
    }

    void add_flight(const A& source, const A& dest, const F& flight) 
    {
        add_airport(source);
        add_airport(dest);

        adjacency_list[source].push_back(make_pair(dest, flight));
    }

    void display()
    {
        for (const auto& [airport, flights] : adjacency_list)
        {
            cout << "From " << airport << ":\n";
            
            for (const auto& [dest, flight] : flights) 
            {
                cout << "  To " << dest << " - Flight : " << flight << "\n";
            }
            
            cout << "\n";
        }
    }
};

int main() 
{
    AirlineNetwork<string, string> info;

    info.add_flight("İstanbul", "Ankara", "TK10111");
    info.add_flight("İstanbul", "Izmir", "TK20211");
    info.add_flight("Ankara", "Izmir", "TK30311");
    info.add_flight("Izmir", "Antalya", "TK40411");
    info.add_flight("Antalya", "İstanbul", "TK50511");

    info.display();

    return 0;
}
*************************************** 
AÇIKLAMA: 
*************************************** 
CEVAP : 
From Antalya:
  To İstanbul - Flight : TK50511

From Izmir:
  To Antalya - Flight : TK40411

From Ankara:
  To Izmir - Flight : TK30311

From İstanbul:
  To Ankara - Flight : TK10111
  To Izmir - Flight : TK20211
***************************************

Graph veri yapısı ile ilgili anahtar kelimeler :

1. Nodes (Vertices):

• Her düğüm(node) tipik olarak bir varlığı, nesneyi veya veri noktasını temsil eder.

• Düğümler neyi temsil ettikleri hakkında ek bilgi sağlamak için etiketlenebilir.

2.  Edges (Arcs/Links):

• Kenarlar düğümler arasındaki bağlantılardır.

• Düğümler tarafından temsil edilen varlıklar arasındaki ilişkileri, etkileşimleri veya bağlantıları temsil ederler.

• Kenalar directed (point from one node to another) ya da undirected (bi-directional) olabilirler.

3.  Types of Graphs:

• Directed Graph (Digraph) : Kenarların tek yönlü bir ilişkiyi gösteren bir yönü vardır.

• Undirected Graph : Kenarların yönü yoktur ve karşılıklı ilişkileri temsil eder.

• Weighted Graph: Her kenarın kendisiyle ilişkili bir ağırlığı veya maliyeti vardır ve genellikle optimizasyon problemlerinde kullanılır.

• Cyclic Graph : En az bir döngü (aynı düğümde başlayan ve biten bir yol) içerir.

• Acyclic Graph : Herhangi bir döngü içermez.

• Connected Graph : Her düğüm çifti arasında bir yol vardır.

• Disconnected Graph : Bir veya daha fazla yalıtılmış alt grafik içerir.

4.  Degree of a Node:

• Bir düğümün derecesi ona bağlı kenarların sayısıdır.

• Yönlendirilmiş bir grafikte, her düğüm için hem iç dereceler (gelen kenarlar) hem de dış dereceler (giden kenarlar) vardır.

5.  Adjacency:

• İki düğümü birbirine bağlayan bir kenar varsa bitişiktir.

• Bitişiklik matrisi veya listesi, bir grafikte hangi düğümlerin bitişik olduğunu temsil etmek için kullanılır.

6.  Path:

• Yol, her bitişik çiftin bir kenarla bağlandığı bir düğüm dizisidir.

• Bir yolun uzunluğu, içerdiği kenarların sayısıdır.

7.  Connected Components:

• Yönlendirilmemiş bir grafikte, bağlı bir bileşen, herhangi iki düğüm arasında bir yolun bulunduğu bir alt grafiktir.

• Bir grafiğin birbirine bağlı birden fazla bileşeni olabilir.

8.  Cycle:

• Döngü, aynı düğümde başlayıp biten, kapalı bir döngü oluşturan bir yoldur.

• Döngüsel olmayan grafiklerin döngüsü yoktur.

9.  Graph Traversal:

• Derinlik öncelikli arama (DFS) ve genişlik öncelikli arama (BFS) gibi grafik geçiş algoritmaları, bir grafiğin düğümlerini ve kenarlarını keşfetmek veya aramak için kullanılır.

10. Graph Representation:

• Graphs, bitişiklik matrisleri, bitişiklik listeleri ve kenar listeleri dahil olmak üzere çeşitli veri yapıları kullanılarak temsil edilebilir.

11. Applications:

• Grafikler, sosyal ağlar, ulaşım ağları, bilgisayar ağları, öneri sistemleri ve daha fazlasını içeren çeşitli uygulamalarda kullanılır.

12. Planar Graphs:

• Bir grafik, uç noktaları dışında herhangi bir kenarın kesişmediği bir düzlem üzerinde çizilebiliyorsa düzlemseldir.

13. Eulerian and Hamiltonian Paths:

• Euler path, bir grafiğin her kenarını tam olarak bir kez ziyaret eden yoldur.

• Hamilton path, bir grafiğin her düğümünü tam olarak bir kez ziyaret eden bir yoldur.